org.jenetics

Class LinearRankSelector<G extends Gene<?,G>,C extends Comparable<? super C>>

java.lang.Object

org.jenetics.ProbabilitySelector<G,C>

org.jenetics.LinearRankSelector<G,C>

All Implemented Interfaces:

Selector<G,C>

public final class LinearRankSelector<G extends Gene<?,G>,C extends Comparable<? super C>>
extends ProbabilitySelector<G,C>

In linear-ranking selection the individuals are sorted according to their fitness values. The rank N is assignee to the best individual and the rank 1 to the worst individual. The selection probability P(i) of individual i is linearly assigned to the individuals according to their rank.

Here n^-/N is the probability of the worst individual to be selected and n⁺/N the probability of the best individual to be selected. As the population size is held constant, the conditions n⁺ = 2 - n^- and n^- >= 0 must be fulfilled. Note that all individuals get a different rank, i.e., a different selection probability, even if the have the same fitness value.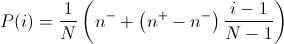

T. Blickle, L. Thiele, A comparison of selection schemes used in evolutionary algorithms, Technical Report, ETH Zurich, 1997, page 37. http://citeseer.ist.psu.edu/blickle97comparison.html

Since:

1.0

Version:

2.0 — $Date: 2014-12-28 $

Author:

Franz Wilhelmstötter

Constructor Summary

Constructors

Constructor and Description
LinearRankSelector() Create a new LinearRankSelector with nminus := 0.5.
LinearRankSelector(double nminus) Create a new LinearRankSelector with the given values for nminus.

Method Summary

Modifier and Type	Method and Description
boolean	equals(Object obj)
int	hashCode()
protected double[]	probabilities(Population<G,C> population, int count) This method sorts the population in descending order while calculating the selection probabilities.
String	toString()

Methods inherited from class org.jenetics.ProbabilitySelector

probabilities, select

Methods inherited from class java.lang.Object

clone, finalize, getClass, notify, notifyAll, wait, wait, wait

Constructor Detail

LinearRankSelector

public LinearRankSelector(double nminus)

Create a new LinearRankSelector with the given values for nminus.

Parameters:

nminus - nminus/N is the probability of the worst phenotype to be selected.

Throws:

IllegalArgumentException - if nminus < 0.

LinearRankSelector

public LinearRankSelector()

Create a new LinearRankSelector with nminus := 0.5.

Method Detail

probabilities

protected double[] probabilities(Population<G,C> population,
                                 int count)

This method sorts the population in descending order while calculating the selection probabilities. (The method Population.populationSort() is called by this method.)

Specified by:

probabilities in class ProbabilitySelector<G extends Gene<?,G>,C extends Comparable<? super C>>

Parameters:

population - The unsorted population.

count - The number of phenotypes to select. This parameter is not needed for most implementations.

Returns:

Probability array. The returned probability array must have the length population.size() and must sum to one. The returned value is checked with assert(Math.abs(math.sum(probabilities) - 1.0) < 0.0001) in the base class.

hashCode

public int hashCode()

Overrides:

hashCode in class Object

equals

public boolean equals(Object obj)

Overrides:

equals in class Object

toString

public String toString()

Overrides:

toString in class Object